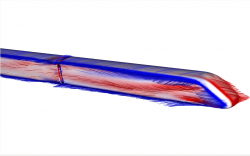
Scenario - Surface Topology
As its name implies, one of FAnToMs main tasks is the computation and analysis of vector field topologies. Therefore, we want to present you one simple scenario to give a first impression of FAnToMs powerfulness. Of course, this is only a small proportion of FAnToMs range of functions.
Basically, the topology of a vector field indicates a subdivision of the corresponding vector field domain in regions with a similar flow behavior. To compute the topology, one has to determine and classify all zeros, also called critical points, of a given vector field. Afterwards, one can compute the topological skeleton by connecting all encountered saddle points with separatrices [HH89]. Since fluid mechanic engineers are, among other things, interested in the development and evolution of vorticies and the separation of the flow from body surfaces, one of the main goals of topological based visualization is to locate and visualize exactly these flow phenomena.
To demonstrate the visualization of a surface topology, we choose a two data sets. One containing a cuboid in a flow an one containing an ICE high speed train. As is well known, flow phenomena are induced by the friction on the body surface. We first visualize the wall shear stress field on the body surface using the so called line integral convolution (LIC) [PW94]. Therefore, the surface is covered with random noise which will be smoothed along the skin friction lines, using a Gaussian kernel for example. As in [PW94] shown, the resulting visualization is comparable with the well studied oil-flow pattern from wind tunnel experiments which allow a good impression of accuring shock waves, vortices and flow separation.
To describe these flow phenomena more precisely, we can now determine and classify all critical points. In our example, we are mainly interested in spiral sinks and in saddle points. In the first case, if the flow converges spirally in one point on the body surface, the flow has no other opportunity than to separate from the surface which generates a vortex perpendicular to the surface in this case [WT+S07] (see Fig. 1). In the second case, one can connect the saddle points by streamlines started along the eigenvectors of the corresponding Jacobian matrices. Theses streamlines are called separatrices and correspond exactly to the hyperbolic skin friction lines which are very well recognizable in the LIC visualization and which anon correspond with flow separation. One could now, for example, use a separatrix as a starting curve of a stream surface to visualize the flow separation with its proceeding into the flow flow domain (see Fig. 2).
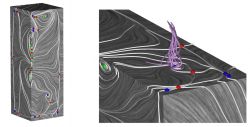
Fig. 1: Swirling streamlines indicating existence of vortex above shear stress field sink (sink is located in lower right part of middle image) (taken from [WTS+07])
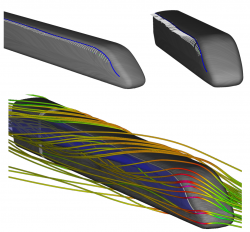
Fig. 2: Separation surface of the ICE train with one separation line and the topological skeletons (taken from [WTS09])
Unfortunately, this works only in the steady case. For time dependent vector fields, still a lot of fundamental research has to be done. Many promising results can be found in literature about the computation and analysis of Finite Time Lyapunov Exponents (FTLE) fields. One approach implemented in FAnToM is for example the computation of an FTLE field on body surfaces combined with a stochastic seeding of pathlines as described in (see Fig. 3).