|
Ralf Der, Thomas Pantzer
Bei der Odometrie, in der Literatur auch als Koppelnavigation oder engl. ``dead reckoning'' bezeichnet, werden Signalgeber an den Rädern benutzt, um den zurückgelegten Weg des Fahrzeugs (Roboter) messen zu können. Die Odometrie ist eine relative Positionsbestimmung. Die neue Position wird dabei aus einer vorher bekannten Position plus zurückgelegter Wegstrecke errechnet. Die Odometrie kann auf kurzen Distanzen sehr genaue Ergebnisse liefern. Allerdings entstehen auch Fehler, die mit zunehmender Entfernung wachsen. Die Räder können rutschen (Schlupf), unrund sein oder unterschiedliche Durchmesser haben (Reifenluftdruck), oder es können durch Bodenunebenheiten falsche Entfernungen gemessen werden. In der Literatur [2], [3] und [4] sind weitere Ansätze zur Selbstlokalisation ausführlich beschrieben.
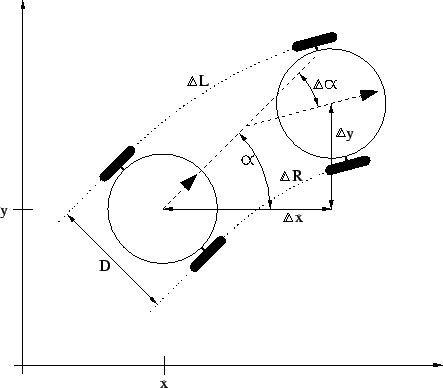
In Abbildung 1 ist die Positionsveränderung
eines zweirädrigen Fahrzeugs im Koordinatensystem schematisch dargestellt. Die Position des Roboters ist durch das Tupel
Der Drehwinkel ![]()
![]() ist die Wegdifferenz des rechten
und linken Rades geteilt durch den Radabstand
ist die Wegdifferenz des rechten
und linken Rades geteilt durch den Radabstand ![]() .
.
Die Wegstrecke ![]() ist der mittlere Weg
ist der mittlere Weg
Die Positionsveräderung bei Geradeausfahrt (
![]() ) ist
) ist
Die Positionsveräderung bei Kurvenfahrt (
![]() und
und
![]() )
ist
)
ist
Unsere Robotik-Experimente führten wir mit einem Modell des Khepera-Roboters durch. Dieser Roboter mißt ca. 50 mm im Durchmesser und besitzt 8 auf den Umfang verteilte Umgebungssensoren die im günstigsten Fall ungefähr 25 mm Reichweite haben. Angetrieben wird der Roboter durch zwei unabhängig steuerbare Schrittmotoren. Die Schrittweite beträgt ca. 0,08 mm.
Das Versuchsgelände bestand aus vier rechtwinklig angeordneten Wänden. Der Roboter wurde mit einem einfachen Controller zur Wandverfolgung programmiert.
Bei Betrachtung des zurückgelegten Weges eines Roboters ist festzustellen, daß sich die Bahnkurve aus Elementen einfacher Kurvenformen zusammensetzen läßt. Die einfachste von ihnen ist die Gerade. Mit dem Anstieg der Geraden ist zugleich eine ganz charakteristische Eigenschaft dieser Spezialform einer ``Kurve'' in nur einem einzigen Wert repräsentiert. Dazu werden noch die Koordinaten eines einzigen Punktes (Startpunkt) und die Länge des Wegstückes benötigt, um diesen Teil der Bahnkurve eindeutig festzulegen.
Wenn dieser Ansatz auf das Prinzip ``Differentialgleichungen beschreiben Kurvenformen'' verallgemeinert wird, können komplizierte Kurvenformen dargestellt und in den meist beschränkten Speichermedien der Roboter-CPU effektiv abgespeichert werden. So kann zum Beispiel während der Verfolgung einer geraden Wand die Lage bzw. die Ausrichtung dieser Wand im Koordinatensystem oder bei der Umrundung eines Hindernisses sein Durchmesser festgestellt werden. Die Odometriedaten des Roboters werden dabei gleichzeitig gemittelt, um eventuelle Schlängelbewegungen des Wandfolgealgorithmus auszugleichen. Der aus den Odometriedaten resultierende Fehler kann klein angenommen werden, da nur die relative Positionsveränderung betrachtet wird.
Die Basis des Algorithmus bildet ein Differentialgleichungsobjekt
![]() .
Es enthält einen Vektor
.
Es enthält einen Vektor
![]() mit allen Ableitungen, zum
Beispiel
mit allen Ableitungen, zum
Beispiel
![]() ,
,
![]() ,
die Wahrscheinlichkeit
,
die Wahrscheinlichkeit ![]() , daß genau dieses Objekt beim nächsten Update
berücksichtigt wird, und die aktuelle Fitness
, daß genau dieses Objekt beim nächsten Update
berücksichtigt wird, und die aktuelle Fitness ![]() bzw. den momentanen
Fehler
bzw. den momentanen
Fehler ![]() . Mehrere Differentialgleichungsobjekte
. Mehrere Differentialgleichungsobjekte ![]() , eine
Abstandsfunktion
, eine
Abstandsfunktion ![]() und die durchschnittliche Fitness
und die durchschnittliche Fitness ![]() bilden nun einen Pool
bilden nun einen Pool
![]() ,
aus dem in jedem Schritt immer ein Objekt herausgegriffen und einem Update unterzogen
wird. Das Objekt mit der höchsten Wahrscheinlichkeit gewinnt den Update seiner
Parameter. Die Wahrscheinlichkeiten der einzelnen Objekte werden nach ihren
Fitnesswerten bzw. Fehlern eingestellt. Dazu wird mit der geeignet gewählten
Abstandsfunktion
,
aus dem in jedem Schritt immer ein Objekt herausgegriffen und einem Update unterzogen
wird. Das Objekt mit der höchsten Wahrscheinlichkeit gewinnt den Update seiner
Parameter. Die Wahrscheinlichkeiten der einzelnen Objekte werden nach ihren
Fitnesswerten bzw. Fehlern eingestellt. Dazu wird mit der geeignet gewählten
Abstandsfunktion ![]() festgestellt, wie gut eine Differentialgleichung
auf das gerade zurückgelegte Wegstück paßt und der zugehörige Fehler ermittelt.
Wenn mehrere Differentialgleichungsobjekte annähernd gleich gut repräsentiert
sind, soll kein Update vorgenommen werden. Nach ausreichend vielen Updateschritten
sind die Koeffizienten konvergiert und die Differentialgleichungen widerspiegeln
die geometrischen Eigenschaften der abgelaufenen Wegstücke.
festgestellt, wie gut eine Differentialgleichung
auf das gerade zurückgelegte Wegstück paßt und der zugehörige Fehler ermittelt.
Wenn mehrere Differentialgleichungsobjekte annähernd gleich gut repräsentiert
sind, soll kein Update vorgenommen werden. Nach ausreichend vielen Updateschritten
sind die Koeffizienten konvergiert und die Differentialgleichungen widerspiegeln
die geometrischen Eigenschaften der abgelaufenen Wegstücke.
Die Differentialgleichung in der Form
![]() ist für unsere
Zwecke ungünstig, da
ist für unsere
Zwecke ungünstig, da ![]() werden kann, wenn die Gerade parallel
zur y-Achse des Koordinatensystems verläuft. Deshalb wird von der gebräuchlichen
Form
werden kann, wenn die Gerade parallel
zur y-Achse des Koordinatensystems verläuft. Deshalb wird von der gebräuchlichen
Form ![]() zur Parameterdarstellung der Gerade übergegangen. Die
Variable
zur Parameterdarstellung der Gerade übergegangen. Die
Variable ![]() ist in diesem Fall die Länge des zurückgelegten Weges auf
der Geraden.
ist in diesem Fall die Länge des zurückgelegten Weges auf
der Geraden.
Mit den Beziehungen aus 9 und 10 läßt sich die folgende Fehlerfunktion
formulieren.
Die Fisher-Eigen-Dynamik [1] beschreibt die Selektionsdynamik in
einem Pool von Individuen unterschiedlicher Fitness ![]() und Wahrscheinlichkeit
und Wahrscheinlichkeit
![]() . Dabei werden die Wahrscheinlichkeiten
. Dabei werden die Wahrscheinlichkeiten ![]() so verändert,
daß nach hinreichend langer Zeit das Individuum
so verändert,
daß nach hinreichend langer Zeit das Individuum ![]() mit der höchsten
Fitness selektiert wird, d.h.
mit der höchsten
Fitness selektiert wird, d.h.
In jedem Zeitschritt wird ein Update für alle Wahrscheinlichkeiten der Differentialgleichungsobjekte
im Pool durchgeführt (Fitness ![]() nach Gleichung 12,
nach Gleichung 12,
![]() ist Anzahl der Differentialgleichungen).
ist Anzahl der Differentialgleichungen).
Gleichzeitig mit dem Update der Wahrscheinlichkeiten ![]() erfolgt ein
Update der Koeffizienten der Differentialgleichungsobjekte zur Minimierung des
Fehlers
erfolgt ein
Update der Koeffizienten der Differentialgleichungsobjekte zur Minimierung des
Fehlers ![]() . Die Größe des Updateschrittes für das Objekt
. Die Größe des Updateschrittes für das Objekt ![]() wird proportional zur Wahrscheinlichkeit
wird proportional zur Wahrscheinlichkeit ![]() gewählt.
gewählt.
Wird der Algorithmus einige Zeit aktiviert, während der Roboter an einer längeren
geraden Wand entlang läuft, werden die Parameter ![]() und
und ![]() sukzessive nachgeführt und spiegeln schließlich den Verlauf der Geraden wider.
Der Vektor
sukzessive nachgeführt und spiegeln schließlich den Verlauf der Geraden wider.
Der Vektor
 aus den gelernten Koeffizienten ist dann ein Einheitsvektor entlang dieser
Geraden.
aus den gelernten Koeffizienten ist dann ein Einheitsvektor entlang dieser
Geraden.
Die Information nach SHANNON [5] dient dazu, Updates zu unterdrücken, falls mehrere Differentialgleichungen ein bestimmtes Wegstück gleich gut repräsentieren.
Ein Update der Koeffizienten wird grundsätzlich nur dann durchgeführt, wenn
![]() kleiner als ein vorgegebener Schwellwert ist. Günstige Werte für diese
Schwelle liegen bei
kleiner als ein vorgegebener Schwellwert ist. Günstige Werte für diese
Schwelle liegen bei
![]() .
In Abbildung 4 ist der Verlauf
.
In Abbildung 4 ist der Verlauf
Wird der Update der Differentialquotienten nicht in einem Schritt vorgenommen,
und das ist der Fall, wenn der Faktor ![]() aus Gleichung 15
kleiner als
aus Gleichung 15
kleiner als ![]() ist, dann erfolgt eine Mittelung über mehrere Zeitschritte.
Ebenso erfahren die Wahrscheinlichkeiten
ist, dann erfolgt eine Mittelung über mehrere Zeitschritte.
Ebenso erfahren die Wahrscheinlichkeiten ![]() aus Gleichung 14
durch den Faktor
aus Gleichung 14
durch den Faktor ![]() eine Mittelung. Das führt dazu, daß die Wahrscheinlichkeiten
erst nach einigen Schritten ihr Maximum erreichen können. Der Update und damit
die Verringerung des Fehlers und Erhöhung der Fitness erfolgen aber nur optimal,
wenn die Wahrscheinlichkeit
eine Mittelung. Das führt dazu, daß die Wahrscheinlichkeiten
erst nach einigen Schritten ihr Maximum erreichen können. Der Update und damit
die Verringerung des Fehlers und Erhöhung der Fitness erfolgen aber nur optimal,
wenn die Wahrscheinlichkeit ![]() über mehrere Schritte einen Wert in der
Umgebung von
über mehrere Schritte einen Wert in der
Umgebung von ![]() aufweist. Nach Gleichung 14 ist die Summe
aller Wahrscheinlichkeiten gleich
aufweist. Nach Gleichung 14 ist die Summe
aller Wahrscheinlichkeiten gleich ![]() , d.h. wenn eine Gleichung eine
Wahrscheinlichkeit von 95% hat, müssen sich alle anderen die restlichen 5%
teilen. Die Wahrscheinlichkeit für eine unpassende Gleichung ist also sehr klein.
Schwenkt der Roboter auf seiner Fahrt jetzt auf eine Bahn, deren zugehörige
Gleichung noch eine niedrige Wahrscheinlichkeit hat, kann es sehr lange dauern,
bis die neue, eigentlich passende Differentialgleichung ein Update erfährt.
Bei sehr kurzen Wegstücken kann es sogar dazu kommen, daß überhaupt kein Update
durchgeführt wird, weil dieses Wegstück bereits wieder verlassen wurde, bevor
die Fisher-Eigen-Dynamik umschlagen konnte.
, d.h. wenn eine Gleichung eine
Wahrscheinlichkeit von 95% hat, müssen sich alle anderen die restlichen 5%
teilen. Die Wahrscheinlichkeit für eine unpassende Gleichung ist also sehr klein.
Schwenkt der Roboter auf seiner Fahrt jetzt auf eine Bahn, deren zugehörige
Gleichung noch eine niedrige Wahrscheinlichkeit hat, kann es sehr lange dauern,
bis die neue, eigentlich passende Differentialgleichung ein Update erfährt.
Bei sehr kurzen Wegstücken kann es sogar dazu kommen, daß überhaupt kein Update
durchgeführt wird, weil dieses Wegstück bereits wieder verlassen wurde, bevor
die Fisher-Eigen-Dynamik umschlagen konnte.
Um diese Verzögerung klein zu halten, wird eine untere Schranke für die Wahrscheinlichkeiten
definiert, die von keinem ![]() unterschritten werden soll. Ist das doch
der Fall, wird das entsprechende
unterschritten werden soll. Ist das doch
der Fall, wird das entsprechende ![]() gleich dem Wert dieser Schranke
gesetzt. Da die Summe aller Wahrscheinlichkeiten
gleich dem Wert dieser Schranke
gesetzt. Da die Summe aller Wahrscheinlichkeiten ![]() gleich
gleich ![]() sein soll ergibt sich eine obere Schranke, die die
sein soll ergibt sich eine obere Schranke, die die ![]() nicht überschreiten
können.
nicht überschreiten
können.
Die Änderungen der Wahrscheinlichkeiten ![]() folgen im Falle eines Umschwenkens
immer den Fitnesswerten nach. In ungünstigen Situationen kann es passieren,
daß die falschen Koeffizienten aufgrund ihrer noch hohen Wahrscheinlichkeitswerte
einen Update mit völlig unpassenden Werten erfahren. Um das zu verhindern, können
folgen im Falle eines Umschwenkens
immer den Fitnesswerten nach. In ungünstigen Situationen kann es passieren,
daß die falschen Koeffizienten aufgrund ihrer noch hohen Wahrscheinlichkeitswerte
einen Update mit völlig unpassenden Werten erfahren. Um das zu verhindern, können
Der zweite Ansatz funktioniert nur unter der Annahme, daß der Roboter sich größtenteils
auf geradlinigen Bahnen bewegt und ein ``Einschwenken'' auf eine andere
Richtung relativ schnell erfolgt. Weiterhin muß nun doch ein Teilstück des zurückgelegten
Weges mit Hilfe von Punktkoordinaten abgespeichert werden. Die gewählte Verzögerung
muß der Weglänge entsprechen, die während der Richtungsänderung zurückgelegt
wird. Der Betrag der Verzögerung kann durch Auswerten der Information nach Shannon
über den Fitnesswerten ![]() und den Wahrscheinlichkeiten
und den Wahrscheinlichkeiten ![]() relativ gut geschätzt werden.
relativ gut geschätzt werden.
Für die Fehlerfunktion wird ein Maß für den Abstand zweier Differentialgleichungen1 benötigt. Die aus dem gerade zurückgelegten Wegstück angenommene Gleichung
soll mit jeder anderen Differentialgleichung verglichen werden. Der größte
erreichbare Abstand soll per Definition den Wert ![]() erhalten. Da in
diesem Spezialfall den Anstieg der Geraden in zwei Variablen (
erhalten. Da in
diesem Spezialfall den Anstieg der Geraden in zwei Variablen (
![]() )
ausgedrückt wird, kann aus deren Vorzeichen auch noch eine Richtung (Vektor)
bestimmt werden. Der Abstand soll den Wert
)
ausgedrückt wird, kann aus deren Vorzeichen auch noch eine Richtung (Vektor)
bestimmt werden. Der Abstand soll den Wert ![]() haben, wenn die zwei Geraden
den größten Abstand voneinander aufweisen, d.h. die Vektoren genau in die entgegengesetzte
Richtung zeigen bzw. einen Winkel von 180
haben, wenn die zwei Geraden
den größten Abstand voneinander aufweisen, d.h. die Vektoren genau in die entgegengesetzte
Richtung zeigen bzw. einen Winkel von 180
![]() einschließen. Bei Identität
soll der Abstand
einschließen. Bei Identität
soll der Abstand ![]() betragen.
betragen.
Die Argumente für die Abstandsfunktion sind die Wegstrecken-Informationen
![]() (oder der Winkel
(oder der Winkel ![]() und die
Weglänge
und die
Weglänge ![]() ) aus einem Zeitschritt
) aus einem Zeitschritt ![]() und die zu lernenden
Werte
und die zu lernenden
Werte
![]() , die den Winkel
, die den Winkel ![]() (Ausrichtung)
der Gerade
(Ausrichtung)
der Gerade ![]() (Kante) im internen Koordinatensystem repräsentieren.
Im ideal gelernten Zustand im Zeitschritt
(Kante) im internen Koordinatensystem repräsentieren.
Im ideal gelernten Zustand im Zeitschritt ![]() sind die folgenden Ausdrücke
äquivalent.
sind die folgenden Ausdrücke
äquivalent.
Es wurden mehrere Abstandsfunktionen getestet.
In Abbildung 6 auf Seite
![[*]](cross_ref_motif.gif) ist der Verlauf der einzelnen
Funktionen an der Stelle
ist der Verlauf der einzelnen
Funktionen an der Stelle
Die Abstandsfunktion nach Gleichung 22 gibt mit der direkten Differenz zwischen zwei Winkeln zwar ein begrifflich sehr gut faßbares Abstandsmaß, benötigt aber den meisten Rechenaufwand. Es lassen sich außerdem Funktionen finden, die steilere Anstiege aufweisen. Im allgemeinen eignen sich Funktionen mit steilen Anstiegen in der näheren Umgebung des Referenzpunktes besser als Abstandsfunktion.
g0r
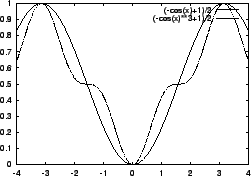 Abstandsfunktion mit steilerem Anstieg
Die Fehlerfunktion nach Gleichung 11 ist im Prinzip eine zwischen
Abstandsfunktion mit steilerem Anstieg
Die Fehlerfunktion nach Gleichung 11 ist im Prinzip eine zwischen
![]() und
und ![]() normierte Kosinusfunktion, die als Argument
den Differenzwinkel der beiden Geraden (Vektoren) hat. Bei der Suche
nach Funktionen mit steileren Anstiegen im Nahbereich fiel die Funktion
normierte Kosinusfunktion, die als Argument
den Differenzwinkel der beiden Geraden (Vektoren) hat. Bei der Suche
nach Funktionen mit steileren Anstiegen im Nahbereich fiel die Funktion
![]() auf. Ein weiterer Vorteil dieser Funktion ist das Plateau bei
auf. Ein weiterer Vorteil dieser Funktion ist das Plateau bei
![]() ,
das bewirkt, daß alle in der näheren Umgebung liegenden Vektoren annähernd gleich
stark berücksichtigt werden und die Entscheidung über den Updatesieger
stärker durch die Wahrscheinlichkeiten
,
das bewirkt, daß alle in der näheren Umgebung liegenden Vektoren annähernd gleich
stark berücksichtigt werden und die Entscheidung über den Updatesieger
stärker durch die Wahrscheinlichkeiten ![]() erfolgt.
erfolgt.
Diese Abstandsfunktion lieferte bei unseren Experimenten die besten Ergebnisse. Bei Richtungsänderungen des Roboters schlugen die Wahrscheinlichkeiten schnell um, und die Anzahl der Fälle, in denen zwei Differentialgleichungsobjekte über einen längeren Zeitraum gleiche Wahrscheinlichkeiten aufwiesen, wurde minimiert.
Nachdem gezeigt wurde, daß das Prinzip der lernenden Differentialgleichungen
für einfache Kurvenformen anwendbar ist, kann zu komplizierteren Kurvenformen
übergegangen werden. Die einfache Gleichung für den Kreisumfang ![]() kann nach
kann nach ![]() umgestellt werden. Der Radius ergibt sich aus dem zurückgelegten
Weg auf der Kreisbahn geteilt durch die Winkeldifferenz in der Ausrichtung.
umgestellt werden. Der Radius ergibt sich aus dem zurückgelegten
Weg auf der Kreisbahn geteilt durch die Winkeldifferenz in der Ausrichtung.
Der Radius einer Kreisbahn ist also der Parameter ![]() , der mit dieser
Differentialgleichung gelernt werden kann. Durch negative Winkel kann der Parameter
, der mit dieser
Differentialgleichung gelernt werden kann. Durch negative Winkel kann der Parameter
![]() auch ein negatives Vorzeichen bekommen. Kreisradien sind aber immer
positiv, das Vorzeichen bezeichnet hier die Richtung, auf der sich der Roboter
auf der Kreisbahn bewegt (positiv = entgegen dem Uhrzeigersinn). Die Werte von
auch ein negatives Vorzeichen bekommen. Kreisradien sind aber immer
positiv, das Vorzeichen bezeichnet hier die Richtung, auf der sich der Roboter
auf der Kreisbahn bewegt (positiv = entgegen dem Uhrzeigersinn). Die Werte von
![]() und
und ![]() können sehr stark fluktuieren. Das
hat zur Folge, daß der Parameter
können sehr stark fluktuieren. Das
hat zur Folge, daß der Parameter ![]() , der ja der Quotient aus
, der ja der Quotient aus ![]() und
und ![]() ist, noch stärkeren Schwankungen unterliegen würde. Um Fehlern
bei der Berechnung im Computer entgegenzuwirken, werden
ist, noch stärkeren Schwankungen unterliegen würde. Um Fehlern
bei der Berechnung im Computer entgegenzuwirken, werden ![]() und
und ![]() als getrennte Variablen im Speicher gehalten. Der Update
der Kreisgleichungsparameter erfolgt (analog zu Gleichung 15) mit dieser
Gleichung:
als getrennte Variablen im Speicher gehalten. Der Update
der Kreisgleichungsparameter erfolgt (analog zu Gleichung 15) mit dieser
Gleichung:
Die Fehlerfunktion soll den Abstand von zwei Kreisradien auf den Wertebereich
![]() abbilden.
abbilden.
Mit dem Parameter ![]() läßt sich die Steilheit bzw. mittlere Breite der
Funktion einstellen und damit die Trennschärfe je nach
Anwendungsgebiet beinflussen oder geeignet auswählen. Im Unendlichen
steigt der Wert der Funktion jeweils auf
läßt sich die Steilheit bzw. mittlere Breite der
Funktion einstellen und damit die Trennschärfe je nach
Anwendungsgebiet beinflussen oder geeignet auswählen. Im Unendlichen
steigt der Wert der Funktion jeweils auf ![]() .
.
Werden Versuche mit verschiedenen Arten von Differentialgleichungsobjekten in
einem Pool ![]() (siehe 2.2) durchgeführt, ist festzustellen,
daß eine Art nur in besonders wenigen Fällen Updates gewinnt.
(siehe 2.2) durchgeführt, ist festzustellen,
daß eine Art nur in besonders wenigen Fällen Updates gewinnt.
So können sich zum Beispiel Differentialgleichungsobjekte für Kreisbahnen nur
dann gegen die für Geraden durchsetzen, wenn wenige andere Differentialgleichungsobjekte
vorhanden sind. Anderenfalls ist der Konkurrenzdruck zu hoch und die Wahrscheinlichkeiten
können sich nicht auf einem Wert stabilisieren, bei dem Updates möglich werden.
Durch die Wahl eines größeren Wertes für ![]() in Gleichung 26
kann zwar der Einzugsbereich für bestimmte Instanzen von Differentialgleichungsobjekten
vergrößert werden, beschränkt aber gleichzeitig die Anzahl der sinnvoll nutzbaren
Objekte. Ein zu großer Wert für
in Gleichung 26
kann zwar der Einzugsbereich für bestimmte Instanzen von Differentialgleichungsobjekten
vergrößert werden, beschränkt aber gleichzeitig die Anzahl der sinnvoll nutzbaren
Objekte. Ein zu großer Wert für ![]() führt allerdings dazu, daß diese eine
Gleichung immer wieder einen sehr hohen Fitnesswert aufweist und damit kein
Umschlagen der Wahrscheinlichkeiten erfolgen kann.
führt allerdings dazu, daß diese eine
Gleichung immer wieder einen sehr hohen Fitnesswert aufweist und damit kein
Umschlagen der Wahrscheinlichkeiten erfolgen kann.
Allgemein kann gesagt werden, daß kompliziertere Kurvenformen seltener einen
Update gewinnen, weil die einfacheren Kurvenformen (z.B. Geraden) in ihnen schon
enthalten sind. Damit weist neben der betrachteten komplizierten Kurvenform
auch immer eine einfache Kurvenform eine relativ hohe Fitness auf, und die Information
nach Gleichung 17 bleibt unter dem Schwellwert für zulässige
Updates. Da sich die Konstruktion von wirklich gleichwertigen Abstandsfunktionen
für verschiedene Klassen von Differentialgleichungsobjekten schwierig
gestaltet, werden immer nur gleichartige Objekte in einer Menge ![]() zusammengefaßt.
zusammengefaßt.
In Abbildung 9a ist der zurückgelegte Weg des Roboters bei einer Versuchsfahrt dargestellt. Ein Skalenteil entspricht dabei einem Millimeter in der wirklichen Welt. Der Roboter wurde auf Wandverfolgung programmiert und hat die aufgebaute Welt (ein Rechteck mit abgerundeten Ecken) 21 mal in einer Richtung umrundet. Dabei wurde nur aus den Odometriedaten der Räder die aktuelle Position des Roboters ca. aller
Durch eine Erweiterung des oben beschriebenen Algorithmus kann zusätzlich zu
den gelernten Bahnparametern ein Driftparameter ![]() gelernt werden,
der die Winkelgeschwindigkeit der virtuellen Rotation des Weltkoordinatensystems
widerspiegelt. Durch Integration von
gelernt werden,
der die Winkelgeschwindigkeit der virtuellen Rotation des Weltkoordinatensystems
widerspiegelt. Durch Integration von ![]() kann zu jedem Zeitpunkt
die aktuelle Verdrehung
kann zu jedem Zeitpunkt
die aktuelle Verdrehung ![]() des Koordinatensystems bestimmt und
damit der systematische Fehler korrigiert werden. Die Parameter
des Koordinatensystems bestimmt und
damit der systematische Fehler korrigiert werden. Die Parameter ![]() und
und ![]() werden in jedem Zeitschritt neu berechnet.
werden in jedem Zeitschritt neu berechnet.
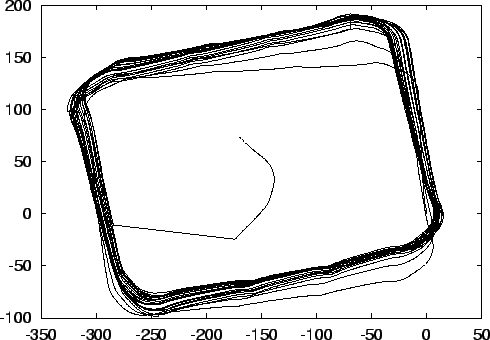
online korrigierte Version der Trajektorie aus Abbildung 9 |
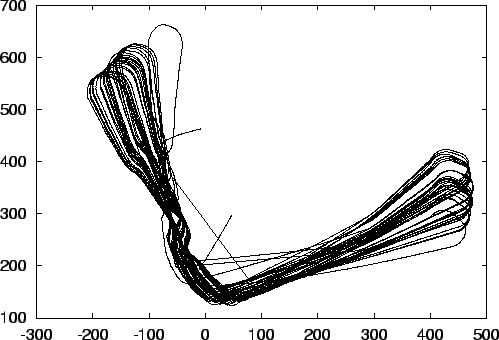
online korrigierte Version der Trajektorie aus Abbildung 10 |
Der vorgestellte Algorithmus hat gezeigt, daß er zur Landmarkenerkennung, speziell zur Erkennung von bestimmten Pfadprofilen, genutzt werden kann. Er ist dabei nicht an das Verfahren der Odometrie gebunden. Die Strukturen der Umgebung (Wände) müssen nicht durch Wandverfolgung ``erlaufen'' werden, sondern können auch das Ergebnis eines Laserscans sein. Werden die Punkte eines Laserscans nach dem Winkel, unter dem sie aufgenommen wurden, sortiert3, ergibt sich annähernd dieselbe Trajektorie wie bei Wandverfolgung4. Mit mehreren aufeinanderfolgenden Scans (auch aus der Bewegung heraus) kann die Orientierung im Raum direkt und kontinuierlich bestimmt werden und man erhält eine Art Kompaß, der sich an den Gegebenheiten des Raumes (z.B. Wände) orientiert.
In [2], Abschnitt 5.3 beschreibt J.S.GUTMANN einen Algorithmus zur Berechnung der Verdrehung eines Laserscans unter Benutzung eines Winkelhistogramms. Der oben beschriebene Algorithmus erzielt in ähnlicher Weise die gleichen Ergebnisse, nur mit dem Unterschied, daß die Winkel direkt aus den Koeffizienten der Differentialgleichungsobjekte abgelesen werden können, ohne daß eine Kreuzkorrelation benötigt wird. Weiterhin sind erste (wenn auch nur partiell korrekte) Ergebnisse schon nach einigen wenigen Updateschritten verfügbar, und eine Erhöhung der Anzahl der Scanpunkte verbessert auch die Genauigkeit, ohne daß signifikant mehr Rechenleistung benötigt wird. Da in jedem Schritt immer dieselben einfachen Operationen durchgeführt werden, kann dieser Algorithmus auch direkt in Hardware realisiert werden.
This document was generated using the LaTeX2HTML translator Version 99.1 release (March 30, 1999)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -html_version 3.2,table -show_section_numbers -split 2 -local_icons -scalable_fonts -numbered_footnotes Diffeq.tex
The translation was initiated by Thomas Pantzer on 2000-09-12