| Definitionen | Kellerautomat,Akzeptierte Sprache, Deterministischer Kellerautomat, deterministisch kontextfreie Sprache,Minimum |
| Simulationen | Kellerautomat |
Zur Beschreibung formaler Sprachen wurden bisher Regelsysteme verwendet, die
formale Sprachen als Wortmengen erzeugen (generieren). Wir betrachten jetzt
Verfahren, mit denen entschieden werden kann, ob ein gegebenes Wort zu einer
bestimmten Sprache gehört. Wir sprechen dann im Gegensatz zur Regelgrammatik,
die die Sprache generiert, von einer akzeptiven Grammatik bzw. von einem
Akzeptor. Wie schon bei endlichen Automaten im Zusammenhang mit regulären
Sprachen geben wir das Verfahren als abstrakte Maschine an.
Dazu erweitern
wir zunächst den Begiff des endlichen Automaten, indem wir neben dem
Eingabespeicher (ROM) einen Lese-Schreib-Speicher (RAM) zur Verfügung stellen,
diesen einschränkend aber wie einen Keller benutzen. Dieser Speicher kann wieder
Wörter über einem (Keller-) Alphabet aufnehmen und über die Operationen
push (Einschreiben in den Keller), pop (Löschen des obersten
Kellerelements) und top (Lesen des obersten Kellerelementes) benutzt
werden. Wenn p, q Wörter über dem Kelleralphabet Y und y Element von Y, dann
gilt für diese Operationen push(p, q) = pq, pop(py) = p und
top(py) = y. Dabei steht das oberste Kellerelement am rechten Ende des
Kellerwortes, d.h. wir lesen den Keller von rechts nach links. (Natürlich kann
das auch umgekehrt festgelegt werden.) Die so festgelegten abstrakten Maschinen
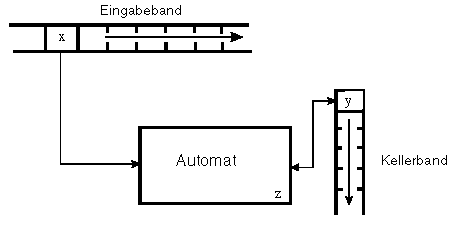
(siehe Schema) werden Kellerautomat genannt.

Bemerkung: Der Kellerautomat ist allgemein nicht-deterministisch.
Arbeitsweise des Kellerautomat K:
Die momentane Situation von K wird durch eine Konfiguration k = ( p,
z, q ) beschrieben, wo p das gegebene Eingabewort (Belegung des Eingabebandes
ab aktueller Position), z den aktuellen Automatenzustand und q das vorliegende
Kellerwort (Belegung des Kellerbandes) angibt.
Die Konfigurationen ( p, z0, S ) heißen Anfangskonfigurationen.
Die Konfigurationen (  , z,
, z,  ) bzw. (
) bzw. (  , zf, q ) mit zf
, zf, q ) mit zf![]() F werden als Endkonfigurationen bezeichnet.
F werden als Endkonfigurationen bezeichnet.
Mit Hilfe der Funktion h wird zu jeder Konfiguration k eine Menge von Folgekonfigurationen
k´ (in Zeichen: k 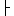 k´) wie folgt bestimmt:
k´) wie folgt bestimmt:
(p, z, q) 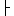 (p´, z´, q´) genau dann, wenn p=xp´, q=q1y,
q´=q1q1´ und (z´, q1´)
(p´, z´, q´) genau dann, wenn p=xp´, q=q1y,
q´=q1q1´ und (z´, q1´) ![]() h(x, z, y)
h(x, z, y)
für y  Y , q1, q1´
Y , q1, q1´ ![]() Y* und x
Y* und x ![]() ( X
( X ![]() {
{![]() } ).
} ).
Durch 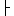 * bezeichnen wir wieder die transitive und reflexive
Hülle von
* bezeichnen wir wieder die transitive und reflexive
Hülle von  und beschreiben damit Konfigurationsfolgen. Dabei ist
k
und beschreiben damit Konfigurationsfolgen. Dabei ist
k 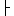 * k´ genau dann, wenn k = k´ oder es gibt eine Folge
k0 ,..., kn von Konfigurationen mit k0 = k
, kn = k´ und ki
* k´ genau dann, wenn k = k´ oder es gibt eine Folge
k0 ,..., kn von Konfigurationen mit k0 = k
, kn = k´ und ki![]() ki+1 für alle 0
ki+1 für alle 0 ![]() i < n.
i < n.
Definition: Akzeptierte Sprache |
Beispiel: Der Kellerautomat K = ( { 0,1 }, { a,b,c }, ( z0,
z1 }, h, z0, a, ![]() ) mit h nach Tabelle
) mit h nach Tabelle
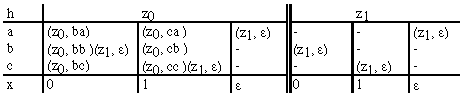
 durch die Konfigurationenfolge (
durch die Konfigurationenfolge ( , z0, a), (
, z0, a), (Von diesem Kellerautomat wird mit leerem Keller die Sprache L ( K ) = { p
( K ) = { p![]()
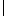 p
p  {0,1}* } akzeptiert. An den nichtdeterministischen
Stellen rät der Automat mit dem Übergang zum Zustand z1 die
Mitte des Eingabewortes. Diese Sprache kann von keinem deterministischen
Kellerautomat akzeptiert werden.
{0,1}* } akzeptiert. An den nichtdeterministischen
Stellen rät der Automat mit dem Übergang zum Zustand z1 die
Mitte des Eingabewortes. Diese Sprache kann von keinem deterministischen
Kellerautomat akzeptiert werden.
 h ( x, z, y ) möglichen Übergängen die mit ( x, y,
q ) beschrifteten Kanten entsprechen.
h ( x, z, y ) möglichen Übergängen die mit ( x, y,
q ) beschrifteten Kanten entsprechen.
Der Kellerautomat aus dem obigen Beispiel ist durch den folgenden Graphen bestimmt.
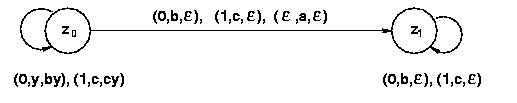
Die Übergänge von z nach z´ für ( z´, q )  h (
h (  , y, z ) heißen
, y, z ) heißen  -Übergänge.
-Übergänge.
|
Beweis:
 } ) simuliert.
} ) simuliert.  zu der neuen Zustandsmenge Z´.
zu der neuen Zustandsmenge Z´.

 }
}
 X, y
X, y  Y, z
Y, z  Z ist h' und h identisch. Lediglich für das neue
Startsymbol und den Anfangszustand zo´ konstruieren wir h´ derart, daß
ausgehend vom Startzustand z0´ und vom Startsymbol S´ in den
Zustand z0 mit der Kellerinschrift S´S übergegeangen wird.
Die neu entstandene Konfiguration ist die Startkonfiguration des Kellerautomat
K. Akzeptiert der Automat K mit leerem Keller, so ergibt sich die Kellerinschrift
von K' zu S´
Z ist h' und h identisch. Lediglich für das neue
Startsymbol und den Anfangszustand zo´ konstruieren wir h´ derart, daß
ausgehend vom Startzustand z0´ und vom Startsymbol S´ in den
Zustand z0 mit der Kellerinschrift S´S übergegeangen wird.
Die neu entstandene Konfiguration ist die Startkonfiguration des Kellerautomat
K. Akzeptiert der Automat K mit leerem Keller, so ergibt sich die Kellerinschrift
von K' zu S´ . Anschließend wird in den Endzustand z
. Anschließend wird in den Endzustand z , z0´, S´) = { (z0, S´S)
},
, z0´, S´) = { (z0, S´S)
},  , z, S´) = { (z
, z, S´) = { (z ,
,  ) },
) },  X, y
X, y  Y, z
Y, z  Z .
Z .  (K´)
(K´)  ´. Das Kelleralphabet Y´ ergibt sich aus dem Kelleralphabet
Y, erweitert um ein neues Startsymbol S´.
´. Das Kelleralphabet Y´ ergibt sich aus dem Kelleralphabet
Y, erweitert um ein neues Startsymbol S´.
 ´
´  ´} und
´} und
 ZF) in einen neuen Zustand z
ZF) in einen neuen Zustand z , z0´, S´) = { (z0, S´S)
},
, z0´, S´) = { (z0, S´S)
},  , z
, z , z, y) = { (z
, z, y) = { (z X, y
X, y  Y, z
Y, z  Z.
Z.
Satz: Kellerautomat und kontextfreie Sprachen
|
 (K) = L . O.B.d.A. können wir voraussetzen, daß
L durch eine Grammatik
(K) = L . O.B.d.A. können wir voraussetzen, daß
L durch eine Grammatik 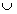 A), {z}, h, z, S,
A), {z}, h, z, S, 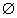 ) mit
) mit  )}, h (
)}, h ( , z, u) = {(z, v)} für x
, z, u) = {(z, v)} für x  A, u
A, u  M und (u, v)
M und (u, v)  R.
R.
Man kann zeigen, daß es zu jeder Linksableitung eines Wortes p aus
L bzgl. G eine Konfigurationsfolge von K gibt, so daß S 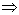 p gdw.
p gdw.
(p, z, S) ![]() * (
* ( , z,
, z,  ) .
) .
Der Kellerautomat simuliert mit den Übergängen ( , u, v) die Linksableitung und schreibt jeweils
das Spiegelbild der durch die Regelanwendung erzeugten Wörter als Zwischenergebnisse
in den Keller. Die Überführung (x, x,
, u, v) die Linksableitung und schreibt jeweils
das Spiegelbild der durch die Regelanwendung erzeugten Wörter als Zwischenergebnisse
in den Keller. Die Überführung (x, x,  ) dient dazu, den Keller von Eingabesymbolen aus
A zu säubern, die bei der Simulation im Keller entstehen. Genauer wird
der Beweis induktiv über die Länge der Ableitung bzw. Konfigurationsfolge
geführt.
) dient dazu, den Keller von Eingabesymbolen aus
A zu säubern, die bei der Simulation im Keller entstehen. Genauer wird
der Beweis induktiv über die Länge der Ableitung bzw. Konfigurationsfolge
geführt.
 (K) die kontextfreie Grammatik G = ( M, X, R, S
) konstruiert , wofür
(K) die kontextfreie Grammatik G = ( M, X, R, S
) konstruiert , wofür 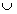 Y
Y 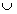 { [ z, y, z´]
{ [ z, y, z´] 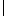 y
y  Y, z, z´
Y, z, z´  Z } und R = RS
Z } und R = RS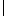
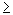 0 , z, z´, zi
0 , z, z´, zi Z, x
Z, x  X
X 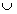 {
{ }, und (zn , y1 ... yn
)
}, und (zn , y1 ... yn
)  h (x, z, y)}.
h (x, z, y)}.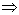 p
p 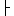 * (
* (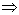 [ z0, S, z´] erzeugt werden kann, folgt
schließlich p
[ z0, S, z´] erzeugt werden kann, folgt
schließlich p  L
L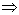 p
p  L
L (K) ist noch eine entsprechende Regel in G zu ergänzen.
(K) ist noch eine entsprechende Regel in G zu ergänzen.
Definition: Deterministischer Kellerautomat, deterministisch kontextfreie Sprache |
Satz: Durchschnitt mit regulären Sprachen
|
 h´( x, y, [ z, z´] ) falls (
h´( x, y, [ z, z´] ) falls ( h ( x, y, z ) und f( x, z´) =
h ( x, y, z ) und f( x, z´) =  h´(
h´( , y, [ z, z´]) falls (
, y, [ z, z´]) falls ( h (
h ( , y, z).
, y, z).
Dann kann man zeigen:
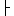 (
(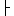 (
(|
Satz: Abgeschlossenheit gegenüber inversen Homomorphismen
|
Beweis: Zu den nach Voraussetzung existierenden (deterministischen) Kellerautomat
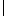 existiert p´
existiert p´

 ] ) = { ( [ z, f (
] ) = { ( [ z, f (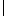

 Y } ,
Y } ,  , y, [ z, p ] } = { ( [
, y, [ z, p ] } = { ( [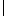 (
( h (
h (  , y, z ) },
, y, z ) },  -Übergänge von K simuliert, bzw
-Übergänge von K simuliert, bzw  , y, [ z, xp ] ) = { ( [ z, p ], q )
, y, [ z, xp ] ) = { ( [ z, p ], q ) 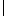 { z, q )
{ z, q )  h ( x, y, z ) },
h ( x, y, z ) },
Dann kann gezeigt werden, daß für zf![]() F gilt:
F gilt:
(p,[z0,![]() ],S)
],S) 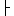 *K'(
*K'(![]() ,[zf,
,[zf,![]() ],q) gdw. (f(p),z0,S)
],q) gdw. (f(p),z0,S) 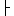 *K(
*K(![]() , zf, q), d.h. LF (K´)=f-1(L).
, zf, q), d.h. LF (K´)=f-1(L).
|
Definition: Min(L)= {p
|
| Satz: Abgeschlossenheit gegenüber Minimumbildung Wenn L deterministisch kontextfrei, dann ist auch Min(L) deterministisch kontextfrei. |
Beweis: Zu dem nach Voraussetzung existierenden deterministischen Kellerautomat
 p
p  { a, b }* } wird durch die Grammatik mit den Regeln
{ a, b }* } wird durch die Grammatik mit den Regeln
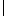 bSb
bSb 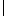
 erzeugt, ist also kontextfrei. Wenn wir annehmen,
daß L deterministisch kontextfrei ist, dann wären L´ = L
erzeugt, ist also kontextfrei. Wenn wir annehmen,
daß L deterministisch kontextfrei ist, dann wären L´ = L 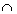 (ab)+ (ba)* (ab)* (ba)+ = {(ab)m
(ba)n (ab)n (ba)m
(ab)+ (ba)* (ab)* (ba)+ = {(ab)m
(ba)n (ab)n (ba)m 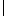 m
m 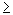 1,n
1,n 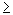 0 } und Min(L´) = { p
0 } und Min(L´) = { p 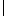 p
p  L´ und
L´ und 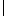 0
0 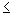 n < m } mit der homomorphen Substitution f (a)
= ab , f (b) = ba folgen würde.
n < m } mit der homomorphen Substitution f (a)
= ab , f (b) = ba folgen würde.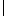 n
n 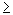 0 } wird von dem deterministischen
0 } wird von dem deterministischen
Satz: Eigenschaften deterministisch kontextfreier
Sprachen
|