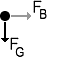
 FG: Gewichtskraft; FB:
Beschleunigungskraft
FG: Gewichtskraft; FB:
BeschleunigungskraftFreier Fall und Schiefer Wurf
Freier Fall
Die Simulation eines freien Falls im Computer ist relativ einfach. Man nimmt zunächst an, dass der Körper nur durch einen Punkt - seinen Schwerpunkt - beschrieben wird. Auf diesen Körper wirkt nun seine Gewichtskraft und er fällt nach unten. Optional kann auch noch eine Beschleunigung in eine andere Richtung erfolgen. Man zerlegt die auf den Körper wirkenden Kräfte in der folgenden Form:
 FG: Gewichtskraft; FB:
Beschleunigungskraft
FG: Gewichtskraft; FB:
Beschleunigungskraft
Hierzu wird angenommen, dass die Erdbeschleunigung (g = 9.807 m/sē) eine Konstante ist. Man berechnet nun den Weg, den der Körper pro Zeiteinheit t (z.B. Sekunden) zurück legt. Anhand der Formeln v = g * t und s = (v * t)/2 kann folgende Formel zur Berechnung des Weges im freien Fall abgeleitet werden:
s = g/2 * tē s=Strecke; g=Fallbeschleunigung; t=Zeit
Bei der graphischen Darstellung des freien Falls subtrahiert man diese Strecke in einer Schleife jedes mal von der y-Koordinate des Körpers. Bei einem Fall von 10 Sekunden also:
| solange t kleiner 10 |
|
s = g/2 * tē //vertikalen Weg berechnen y = y - s //vertikale Bewegung ausführen t = t + 1 |
Die Schleife muss logischerweise eine Abbruchbedingung enthalten. Im obigen Fall begrenze ich die Zeit; besser wäre allerdings, die Schleife abzubrechen, sobald sich die y-Koordinate aus dem sichtbaren Bereich bewegt.
Wirkt auf den Körper zusätzlich eine Beschleunigungskraft FB nach rechts, so entspricht dies durch die Formel F = m * a = m * v * t (a = Beschleunigung) einer Geschwindigkeit nach rechts. Nun berechnet man nach jedem Zeitintervall den zurückgelegten Weg auf der x-Achse:
| solange Zeit kleiner 10 |
|
sV = g/2 * tē //freier Fall y = y - sV //vertikale Bewegung sH = v * t //Rechtsbewegung x = x + sH //horizontale Bewegung t = t + 1 //Die Zeit läuft weiter |
Für v = 4m/s würde das folgende Parabel ergeben:

Bei v = 0 wäre die Parabel logischerweise eine gerade Linie.
 Quellcode
herunterladen (C++-Quellcode; WinAPI)
Quellcode
herunterladen (C++-Quellcode; WinAPI)
 Programm
herunterladen (.zip-Datei, Windows)
Programm
herunterladen (.zip-Datei, Windows)
Schiefer Wurf
Für den schiefen Wurf ergibt sich zum Beispiel die folgende Wurfparabel:

Ein Körper wird mit einer bestimmten Geschwindigkeit nach oben und nach rechts geschleudert. Die Gewichtskraft des Körper wirkt der vertikalen Geschwindigkeit entgegen und er fällt irgendwann zu Boden. Im Programm erhalten die Richtungen (x, y) je eine Geschwindigkeit (vx, vy). Die Geschwindigkeit nach oben wird abgebremst; sie verlangsamt sich. Am höchsten Punkt der Wurfparabel kehrt sie sich letztendlich um und beschleunigt nun in die entgegengesetzte Richtung zum Boden hin.
| solange Körper innerhalb sichtbarem Bereich |
|
sH = vx * t //horizontalen Weg berechnen x = x + sH //horizontale Bewegung ausführen sV = vy * t //vertikalen Weg berechnen y = y + sV //vertikale Bewegung nach oben ausführen sG = g/2 * tē //Gewichtskraft y = y - sG //vertikale Bewegung nach unten ausführen t = t + 1 //Zeit erhöhen |
 Quellcode herunterladen (C++-Quellcode; WinAPI)
Quellcode herunterladen (C++-Quellcode; WinAPI)
 Programm
herunterladen (.zip-Datei, Windows)
Programm
herunterladen (.zip-Datei, Windows)
Anmerkung: Selbstverständlich simulieren die Programme keine realen Fälle und Würfe: Zum einen fehlt die Berechnung des Luftwiderstandes. Außerdem ist ein realer Körper nicht homogen (gleichförmig) und dreht sich während des Fluges.
 |