Flächeninhalt von Integralen

Berechnung des Flächeninhaltes von Integralen

über rechteckige Unterteilungen

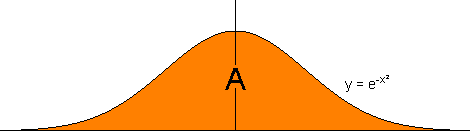
Die Aufgabe ist, den Flächeninhalt einer unregelmäßigen, zusammenhängenden Fläche, unterhalb einer vorgegeben Funktion, zu bestimmen:

Graph der Funktion y = e^(-x²)

Der Flächeninhalt des orange gefärbten Bereiches ist gesucht. Um einen Näherungswert für diesen Flächeninhalt zu erhalten, wird die Fläche in Rechtecke gleicher Breite unterteilt, von denen man den Flächeninhalt sehr einfach ausrechnen kann:

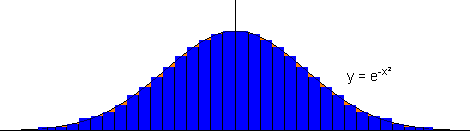
Graph der Funktion y = e^(-x²) mit Unterteilungen

Man berechnet nun in einer Schleife einfach den Flächeninhalt jedes Rechteckes und addiert ihn zum Gesamtflächeninhalt. Man kann den Flächeninhalt auch eingrenzen, indem man einen "Start"- und einen "Zielpunkt" setzt:

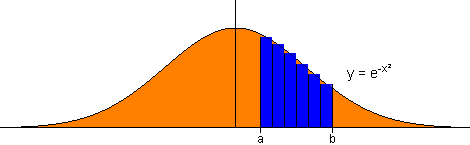
Graph der Funktion y = e^(-x²); nur teilweise unterteilt

Die Linien senkrecht auf a und b begrenzen nun zusammen mit der y-Achse (unten) und der Funktion (oben) eine Fläche, deren Flächeninhalt mit Hilfe der rechteckigen Unterteilungen berechnet werden soll. Für die Funktion y = e^-x² wäre das folgende Schleife:

x = a+(BreiteProRechteck/2); x<b; x=x+BreiteProRechteck

y = e^-x²
A = A + (BreiteProStreifen*y) //Flächeninhalt der Unterteilungen

Die Breite pro Rechteck erhält man einfach, indem man die linke Begrenzung (a) von der rechten Begrenzung (b) subtrahiert und das ganze durch die Anzahl aller Unterteilungen (N) teilt: BreiteProRechteck = (b-a) / N.

Diese Schleife beginnt bei x = a + (BreiteProRechteck/2), da wir von jedem Rechteck den Mittelpunkt auswählen. Das ist nötig, damit die Unterteilung sozusagen mit dem oberen, mittleren Punkt an die Funktion stößt (s. Bilder oben). Würde man mit x = a beginnen, so würden die rechteckigen Unterteilungen mit ihrem linken, obersten Punkt an die Funktion stoßen und ein großer Teil würde "überstehen".

Je mehr Unterteilungen das Programm macht, desto genauer wird der berechnete Näherungswert für den Flächeninhalt. Der vollständige Flächeninhalt der Funktion y=e^-x² über die gesamte reelle Achse ist 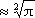~ SQRT(Pi) . Folgende Tabelle zeigt den Näherungswert des Flächeninhaltes in Abhängigkeit der Anzahl der Unterteilungen für a= -100 und b=100:

Unterteilungen	2	10	100	150	200	500
Flächeninhalt	100	20	2,073	1,786	1,77264	1,7724...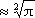

Quellcode herunterladen (C++-Quellcode)
Programm herunterladen (.zip-Datei, DOS)

Anmerkung: Im Quellcode-Paket ist eine Datei namens "main_polynom.cpp" enthalten. Sie beinhaltet den Quellcode des Programms für Polynomfunktionen.