Inhalt

5 Datendarstellung im Rechner

Ein Programm ist ein codierter Algorithmus.

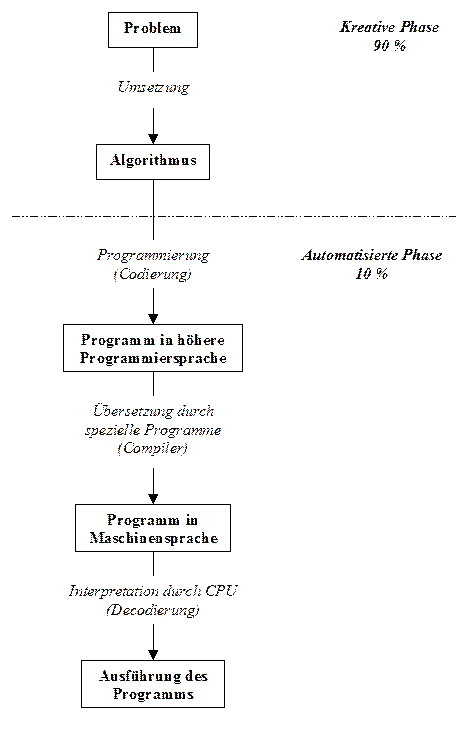
Algorithmen dienen i.R. der Manipulation mathematischer Objekte. Sowohl die Objekte als auch der Algorithmus sind somit zu codieren.

Die Daten und Programme sollten weitestgehend mit den Objekten und den Algorithmen verträglich sein, d.h.

mit ,

wobei hier , , die Objekte, die Codierungsfunktion, + für eine beliebige Operation und Å für deren Interpretation im Rechner steht.

Durch die Endlichkeit des Rechners bestehen Einschränkungen im Wertebereich der darstellbaren Objekte und es werden mathematische Gesetze verletzt!

=> fehlerbehaftete Daten, Verfahrensfehler

=> fehlerbehaftete Ergebnisse

=> Numerik

Wir wollen uns der Frage zuwenden, wie weit Computerergebnisse überhaupt brauchbar sind.

Beispiel aus terms_a.c

float a = 1e10, b = 1e10, c = 1e-10;

printf( "%f\n", a * ( a - b + c));

/* a*((a-b)+c) => 1 */

printf( "%f\n", a * ( a + c - b));

/* a*((a+c)-b) => 1 */

/* Rechner => 0 */

Beispiel aus terms_b.c

int x = 40, y; float a = 1e10;

y = a * x; printf( "%d\n", y);

/* y=1e10*40 => 4e11 */

/* Rechner => 2147483647 */

5.1 Positionssysteme

Der Zahlenwert ist abhängig von der Position der Ziffern in der Zahlendarstellung.

Ziffern

Endliche Menge von mindestens 2 Zeichen Z

Ziffer i.d.R. hindu-arabische Ziffern

ausgezeichnetes Element

Basis Anzahl der Ziffern

Wert einer Ziffer ist eine eindeutige Abbildung, welche jeder Ziffer eine Zahl zuordnet.

natürliche Zahlen

Zahlendarstellung , wobei

Zahlenwert

Beispiel im Dualsystem

137 = 128 + 8 + 1 = 1 * 2⁷ + 1 * 2³ + 1 * 2⁰ = (1000 1001)₂ = (211)₈ = (89)₁₆

137 : 2 = 68 Rest 1

68 : 2 = 34 Rest 0

34 : 2 = 17 Rest 0

17 : 2 = 8 Rest 1

8 : 2 = 4 Rest 0

4 : 2 = 2 Rest 0

2 : 2 = 1 Rest 0

1 : 2 = 0 Rest 1

rationale Zahlen

Zahlendarstellung

mit und

Zahlenwert

mit

und

Beispiel im Dualsystem

3.15625 = 3 + 0.15625 = (11)₂ + (0.00101)₂ = (11.00101)₂

0.15625 * 2 = 0.31250

0.3125 * 2 = 0.625

0.625 * 2 = 1.25

0.25 * 2 = 0.5

0.5 * 2 = 1

5.2 Codierung natürlicher Zahlen

unsigned char, unsigned short int,

unsigned int, unsigned long int

Wegen der Endlichkeit des Speichers kann nur ein Teil der natürlichen Zahlen als sogenannter direkter Code im Rechner dargestellt werden.

Direkter Code - Dualdarstellung mit festgelegter Bitanzahl:

Natürliche Daten werden als ihre Dualdarstellung in den für den Datentyp vorgesehenen Speicherbereich abgespeichert, wobei, je nach Länge der Dualzahl, mit Nullen auf die Bitanzahl des Datentyps aufgefüllt wird.

Die verwendete Bitanzahl n für die Datentypen legen die Grenzen der Zahlendarstellung fest.

unsigned char => n = 8

Dualdarstellung: 59 = (11 1011)₂

unsigned char z = 59; 0011 1011

unsigned char UCHAR_MAX = 255; 1111 1111

unsigned char UCHAR_MIN = 0; 0000 0000

(vgl. Anhang A)

Darstellbarer Zahlenbereich: =>

Darstellbare natürlichen Zahlen mit maximal 4 Bit (n = 4):

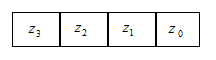
Dezimalzahl	Computerzahl	Berechnung
0	0000	0
1	0001
2	0010
3	0011
4	0100	...
5	0101	...
6	0110	...
7	0111
8	1000
9	1001	...
10	1010	...
11	1011	...
12	1100	...
13	1101	...
14	1110	...
15	1111

5.3 Codierung ganzer Zahlen

signed char, signed short int,

signed int, signed long int

Wegen der Endlichkeit des Speichers kann nur ein Teil der ganzen Zahlen als direkter Code bzw. dessen Komplement im Rechner dargestellt werden.

Direkter Code - Dualdarstellung mit festgelegter Bitanzahl

Komplementdarstellung des direkten Codes von | z |

Komplementbildung:

signed char => n = 8, 8. Bit ist Vorzeichenbit s.

Dualdarstellung: 59 = (11 1011)₂

signed char z = 59; 0011 1011

signed char z = -59; 1100 0001

signed char CHAR_MAX = 127; 0111 1111

signed char CHAR_MIN = -128; 1000 0000

(vgl. Anhang A)

Darstellbarer Zahlenbereich: =>

Darstellbare ganzen Zahlen mit maximal 4 Bit (n = 4):

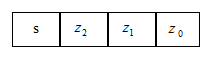
Dezimalzahl	Computerzahl	Berechnung
7	0111
6	0110
5	0101	...
4	0100	...
3	0011	...
2	0010	...
1	0001
0	0000	0
-1	1111
-2	1110
-3	1101	...
-4	1100	...
-5	1011	...
-6	1010	...
-7	1001
-8	1000

Beispiel aus terms_b.c

int x = 40, y; float a = 1e10;

y = a * x; printf( "%d\n", y);

/* y=1e10*40 => 4e11 */

/* Rechner => 2147483647=2^31-1=INT_MAX */

5.4 Codierung rationaler Zahlen

float, double, long double

Wegen der Endlichkeit des Speichers kann nur ein Teil der rationalen Zahlen als sogenannte Gleitpunktzahlen im Rechner dargestellt werden.

Darstellung einer rationalen Zahl als Gleitpunktzahl mit Mantisse M und Exponent E:

1. Ausgangspunkt ist die Dualdarstellung der Zahl.

3.15625 = 3 + 0.15625 = (11)₂ + (0.00101)₂ = (11.00101)₂

2. Einführung der wissenschaftlichen Notation.

Es erfolgt eine Normalisierung durch Stellenverschiebung auf 1. ^{.
. .} , man erhält eine Mantisse M und einen Exponenten E:

(11.00101)₂ = (1.100101)₂ * (10)₂ = (1.100101)₂ * 2¹ => M = (1.100101)₂, E = 1

3. Darstellung als Maschinenzahl.

Die Mantisse M ist in ihrer Stellenzahl t beschränkt. Sie wird auf die entsprechende Stellenzahl gerundet. Da die Mantisse stets mit 1. beginnt, lässt man aus Platzgründen diese 1 weg (hidden bit):

M ≈ 1.M’

Exponenten E sind nur bis zu einer festgelegten Größe darstellbar, E Î [ r, R]. Es können nicht beliebig kleine und beliebig große Zahlen dargestellt werden. Die Exponenten werden durch Addition einer Konstanten in den positiven Bereich verschoben:

E’ = E + C > 0 => C = - r + 1

Maschineninterne Darstellung: mit s als Vorzeichenbit + .. 0; - .. 1.

s | E’| M’

Eine Sonderbehandlung erfährt die Zahl 0, sie wird nur durch Nullen codiert:

0 | 0...0 | 0...0

Die Menge der Maschinenzahlen ist durch die Stellenzahl t der Mantisse und durch den kleinsten und größten darstellbaren Exponenten r und R eindeutig bestimmt.

M_z( t, r, R)

Beispiel Mz( 3, -1, 1): Darstellbare positive rationale Zahlen mit 5 Bit

(1 Vorzeichenbit, 2 Exponentenbits und 2 Mantissenbits):

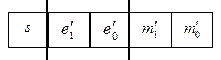
mit M ≈ 1,M’ und mit E’ = E + 2.

z = 3.15625 = (11.00101)₂

=> Mantisse M = (1,100101)₂ , Exponent E = 1

=> M’ = (10)₂ , E’ = 3

=> Interne Darstellung: 0 | 11 | 10

=> z' = (1.10)₂ * 2¹ = (11)₂ = 3, d.h. intern wird 3.15625 auf 3 gerundet!

Übersicht über alle darstellbaren positiven rationalen Zahlen mit 5 Bit als Maschinenzahlen

Mz( 3, -1, 1)

Maschinenzahl	Wert	interne Darstellung
(0.00)₂ * 2 ⁰	= 0	0 \| 00 \| 00
(1.00)₂ * 2^-1	= 4/8	0 \| 01 \| 00	MIN
(1.01)₂ * 2^-1	= 5/8	0 \| 01 \| 01
(1.10)₂ * 2^-1	= 6/8	0 \| 01 \| 10
(1.11)₂ * 2^-1	= 7/8	0 \| 01 \| 11
(1.00)₂ * 2⁰	= 8/8	0 \| 10 \| 00
(1.01)₂ * 2⁰	= 10/8	0 \| 10 \| 01
(1.10)₂ * 2⁰	= 12/8	0 \| 10 \| 10
(1.11)₂ * 2⁰	= 14/8	0 \| 10 \| 11
(1.00)₂ * 2¹	= 16/8	0 \| 11 \| 00
(1.01)₂ * 2¹	= 20/8	0 \| 11 \| 01
*(1.10)₂ 2¹**	= 24/8	0 \| 11 \| 10	⇒z'
(1.11)₂ * 2¹	= 28/8	0 \| 11 \| 11	MAX

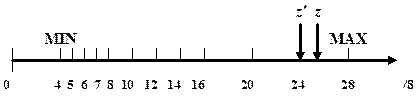
Der Zahlenstrahl mit den darstellbaren Zahlen lässt erkennen, dass es Bereiche gibt, in denen Zahlen nicht darstellbar sind und dass die Abstände der darstellbaren Zahlen von MIN nach MAX größer werden.

Die gleichen Aussagen treffen auch für die negativen Gleitpunktzahlen zu.

Zusammenfassung

1. Wertebereich für Gleitpunkttypen:

, vgl. Kapitel 2:

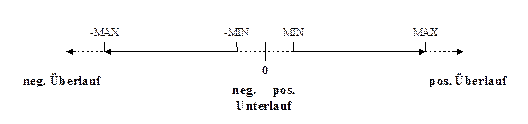
2. Gleitpunktzahlen werden mit zunehmender Größe dünner darstellbar.

3. Je größer Mantissenstellenanzahl t, desto dichter die Zahlendarstellung.

4. Das Intervall [r, R] der Exponenten bestimmt die größte und die kleinste darstellbare Zahl.

Behandlung nicht darstellbarer Zahlen:

1. z > MAX oder z < -MAX:

Überlauf ( Infinity, -Infinity) ⇒ Abbruch: Laufzeitfehler

2. -MIN < z < 0 oder 0 < z < MIN:

Unterlauf ⇒ Sonderbehandlung, Runden auf darstellbare Zahlen: Rundungsfehler

3. -MAX < z < -MIN oder MIN < z < MAX:

Maschinenzahlbereich ⇒ Runden auf darstellbare Zahlen: Rundungsfehler

Standard für rationalen Zahlenbereiche:

(IEEE – Standard[1], Institute of Electrical and Electronics Engineers)

32 – Bit – Format ( 4 Byte) für einfach genaue Zahlen oder auch „single“

64 – Bit – Format ( 8 Byte) für doppelt genaue Zahlen oder auch „double“

80 – Bit – Format ( 10 Byte) für erweitert genaue Zahlen oder auch „double-extended“

Bezeichnung	Byteanzahl	s [Bit]	M [Bit]	E [Bit]	r	R	C
single	4	1	24	8	-126	127	127
double	8	1	53	11	-1022	1023	1023

s	Vorzeichenbit: 0 ... +, 1 ... -	r	kleinster Exponent
M	Länge der Mantisse, einschließlich hidden bit	R	größter Exponent
E	Anzahl der Exponentenbit	C	Verschiebungskonstante

Sonderbehandlung:

M' = 0

M' ≠ 0

E' = 0 (E = r - 1)

z = 0.0

z = ( -1)^s * 2^r * (0.M’)₂;

zusätzliche Zahlen im Unterlauf

E' = E'_max (E = R + 1)

z = ( -1)^s * ∞;

-Infinity, Infinity

NaN (Not a Number);

keine gültige Gleitpunktzahl

C, Java:

Typ	float ⇒ single	double
MAX < 2^R⁺¹	±3.40282347 E +38	±1.797693138462315750 E +308
MIN = 2^r	±1.17549435 E -38	±2.225073858507201383 E -308
Unterlauf (Sonderbehandlung)	±1.40239846 E -45	±4.940656458412465 E -324
gültige Dezimalstellen	7	15

Beispiel für single-Zahlendarstellung(C, Java: float):

Dezimalzahl => Maschinenzahl

3.15625 = (11.0010 1)₂ = (1.1001 01)₂ * 2¹

⇒ M’ = 1001 01, E’ = E + C = 1 + 127 = 128

⇒ 0|100 0000 0|100 1010 0000 0000 0000 0000

0.1 = ()₂ = ()₂ * 2^-4

⇒ M’ = 100 1100 1100 11001100 1100, E’ = E + C = -4 + 127 = 123

⇒ 0|011 1101 1|100 1100 1100 11001100 1100

⇒ Die Zahl 0.1 ist als Maschinenzahl nicht exakt darstellbar.

Maschinenzahl => Dezimalzahl

1|011 1111 1|000 0000 0000 0000 0000 0000

⇒ M’ = 0, E’ = 127 ⇒ M = 1.0, E = E’ - C = 127 + 127 = 0

⇒ -1. * 2⁰ = -1.0

Intern sind Datendarstellungen fehlerbehaftet.

Beispiel aus terms_a.c

float a = 1e10, b = 1e10, c = 1e-10;

printf( "%f\n", a * ( a - b + c));

/* a*((a-b)+c) => 1 */

printf( "%f\n", a * ( a + c - b));

/* a*((a+c)-b) => 1 */

/* Rechner => 0 */

/* Addition sehr groesser mit sehr kleiner Zahl */

Beispiel fraction.c liefert durch Umformen des Bruchs in unterschiedliche Ergebnisse:

fraction.out

x: -10.000000, f: 1.246914, g: 1.246914

. . .

x: -1.500000, f: 13.000000, g: 13.000000

x: -1.000000, f: -Inf, g: Inf

x: -0.500000, f: 5.000000, g: 5.000000

x: 0.000000, f: 1.000000, g: 1.000000

x: 0.500000, f: 0.555556, g: 0.555556

x: 1.000000, f: NaN, g: 0.500000

x: 1.500000, f: 0.520000, g: 0.520000

. . .

x: 10.000000, f: 0.834711, g: 0.834711

Inf ≙ ∞, positiver Überlauf

-Inf ≙ -∞, negativer Überlauf

NaN ≙ Not a Number

[1] http://www.h-schmidt.net/FloatApplet/IEEE754de.html