Fast, GPU-based Therapeutic Ultrasound Beam Simulation

Purpose

This software provides functions for the fast, hardware-accelerated simulation of therapeutic ultrasound beams. The package consists of C/C++ libraries with a MATLAB interface and interface functions to FOCUS.

The software is developed at the Ferrarra Laboratory in the Department of Biomedical Engineering at the University of California at Davis and is supported by NIH3R21EB009434 and by ARRA supplement 3R21EB009434-01S1.

Download

Please read the Copyright.txt provided with the binaries for licensing questions.

Current Release:

Mac OSX 10.6, Intel 32 Bit (dmg/mpkg) [abt. 30MB] [md5: 48234cce15d2d4f2436810a654a94c26 ]
Windows, x84 32 Bit (ZIP) [abt. 30MB] [md5: 8569ebd424179f0181f919398949f7b3 ]

Release History

Version	Date	Comment
0.0.2	2011-01-09	Added Windows and Linux versions.
0.0.1	2010-11-09	Initial Release of OSX version.

Installation

For all platforms, you have to install the cuda drivers and toolkit need a current MATLAB version. Some platforms have special requirements:

Mac OSX

You will need an Intel Macintosh computer that has a reasonably current NVIDIA graphics processor installed. All modern MacBook Pro's should be sufficient.

Windows

A current version of Matlab is sufficient for the non-GPU version of the software. To run GPU-based code, you need NVIDIA's libraries and a compatible graphics board installed.

Linux

The binary requires a 64bit linux system and has been compiled on an Ubuntu Linux system.

Usage

The binary files above provide the required MATLAB binary libraries to reproduce the calculations presented in our publications as well as to conduct your own simulations.

We provide two user interfaces to our code: A native interface (indicated by the ML prefix) and an interface that tries to replicate the function calls of FOCUS. If you use the FOCUS interface, ensure that you have FOCUS installed and running on your machine. In case of OSX, where no FOCUS binaries are provided, our functions can be used to replace some of FOCUS' functionality. The examples below only use FOCUS' MATLAB files and do not rely on the binaries.

The code shown in blue boxes shows our native interface, the code shown in green boxes uses FOCUS' interface.

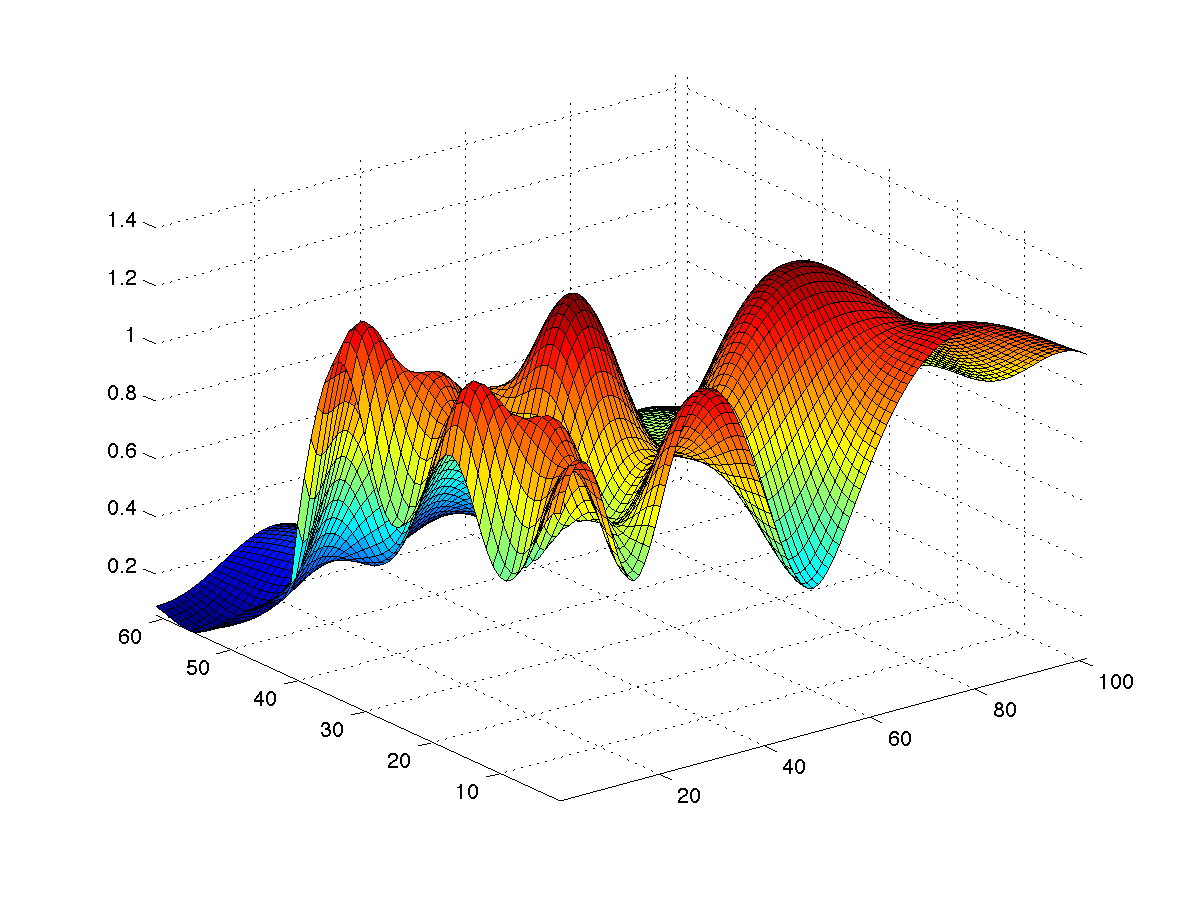
Rectangular Piston

Get information about the interface:

MLRectangularPistonGrid
??? Error using ==> MLRectangularPistonGrid
Must have five or six input arguments: ([4x4 transform], [sx, sy, sz], l, s, k, ['cuda'|'cudadp'|'cpu'|'cpusp'|'cpudp'], [nabscissas])

Compute the near-field in front of a piston:

%% setup the basic parameters
f0=1540000; % excitation frequency (Hz)
c=1500; % speed of sound (m/s)
lambda = c/f0; % wavelength (m)
k=2*pi/lambda; % wavenumber (1/m)
rho=1000; % acoustic density

%% setup piston parameters and the computational grid
s=5.0*lambda; % piston width
l=7.5*lambda; % piston height
siz = [ 61 1 101 ]; % grid sizes
sampling = [s/2/(siz(1)-1)/2*3 1 s*s/4/lambda/(siz(3)-1)];
transform = [ sampling(1) 0 0 0; 0 sampling(2) 0 0; 0 0 sampling(3) 0; 0 0 0 1 ];

%% do the calculation
pressure = MLRectangularPistonGrid( transform, siz, l, s, k, 'cuda', 40)*(1j*c*rho);

%% display and store the result
figure(1); surf(abs(squeeze(pressure))); axis tight
saveas(figure(1), 'figure1.png')

%% setup the basic parameters
f0=1540000;
define_media;
lambda = lossless.soundspeed/f0;

%% setup piston parameters and the computational grid
s=5.0*lambda;
l=7.5*lambda;
siz = [61 1 101];
sampling = [s/2/(siz(1)-1)/2*3 1 s*s/4/lambda/(siz(3)-1)];
ps=set_coordinate_grid(sampling,0,1.5*s/2,0,0,0,s^2/4/lambda);
transducer=get_rect(s/2, l/2, [0 0 0], [0 0 0]);

%% do the calculation
pressure=gpu_fnm_call(transducer,ps,lossless,40,f0,0);

%% display and store the result
figure(1); surf(abs(squeeze(pressure))); axis tight
saveas(figure(1), 'figure1.png')

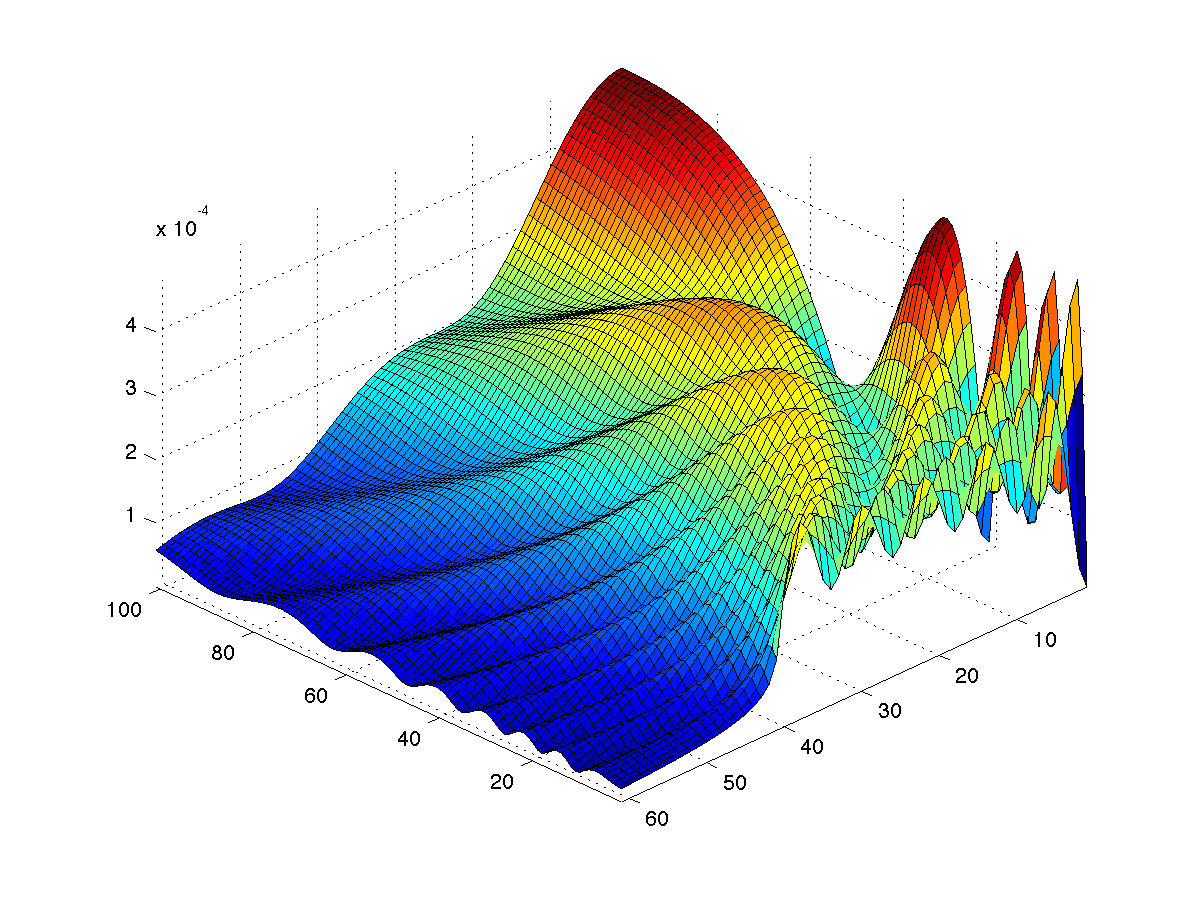
This should result in a picture file called "figure1.png" that looks as follows:

Circular Piston

If you want to compute the circular piston described in McGough's paper on the cpu, then use

MLCircularPistonGrid
??? Error using ==> MLCircularPistonGrid
Must have four or five input argument: (transform4x4, [sizex, sizey, sizez], radius, k, [, 'cuda' | 'gpu',[ abscissas]]

with the following parameters

f0=1000000; % excitation frequency
c=1500; % speed of sound
lambda = c/f0; % wavelength
k=2*pi/lambda; % wavenumber
radius=5.0*lambda; % piston radius
siz = [ 61 1 101 ];
sampling = [1.5*radius/(siz(1)-1) 1 radius^2/lambda/(siz(3)-1)];
transform = [ sampling(1) 0 0 0; 0 sampling(2) 0 0; 0 0 sampling(3) 0; 0 0 0 1 ];
rho=1000;
pressure = MLCircularPistonGrid( transform, siz, radius, k, 'cpu', 40)*(1j*rho*c);
figure(2); surf(abs(squeeze(pressure))); axis tight; view(225,45);
saveas(figure(2), 'figure2.png')

f0=1540000;
define_media;
lambda = lossless.soundspeed/f0;
radius=5.0*lambda;
siz = [61 1 101];
sampling = [1.5*radius/(siz(1)-1) 1 radius^2/lambda/(siz(3)-1)];
ps=set_coordinate_grid(sampling,0,sampling(1)*(siz(1)-1),0,0,0,sampling(3)*(siz(3)-1));
transducer=get_circ(radius, [0 0 0], [0 0 0]);
pressure=cpu_fnm_call(transducer,ps,lossless,40,f0,0);
figure(2); surf(abs(squeeze(pressure))); axis tight; view(225,45);
saveas(figure(2), 'figure2.png')

which should result in a picture file called "figure2.png" that looks as follows:

Regular Piston Arrays

Arrays of pistons are calculated by first computing a larger single-piston solution and then computing a convolution with the piston pattern. We start by computing the piston from above at an extended 256-wide grid and do a convolution in x direction, where each piston has a center-center distance to its neighbor of 64 grid points, i.e., 64/61*radius.

%% setup parameters
f0=1000000; % excitation frequency
c=1500; % speed of sound
lambda = c/f0; % wavelength
k=2*pi/lambda; % wavenumber
radius=5.0*lambda; % piston radius
siz = [ 256 1 101 ];
sampling = [1.5*radius/(61-1) 1 radius*radius/lambda/(siz(3)-1)];
transform = [ sampling(1) 0 0 0; 0 sampling(2) 0 0; 0 0 sampling(3) 0; 0 0 0 1 ];

%% compute a single piston
pressure = MLCircularPistonGrid( transform, siz, radius, k, 'cpu', 40);
figure(2); surf(abs(squeeze(pressure))); axis tight; view(225,45);
saveas(figure(2), 'figure2.png')

%% compute the convolution of four elements, triggered synchronously
array_pressure = MLRectilinearArrayConvolution( pressure, [1; 1; 1; 1], 4, 1, 64, 1, 'cuda')
%% draw figure
figure(3); surf(abs(squeeze(array_pressure))); axis tight; view(225,45);
saveas(figure(3), 'figure3.png');

The result is a 64x1x101 grid that is aligned with the outer of the four pistons as shown here:

Keep in mind that any call to MATLAB involves copying data from MATLAB to C/C++ to the GPU. This may slow down some operations tremendously.

Publications

	Fast ultrasound beam prediction for linear and regular two-dimensional arrays using a general-purpose graphics processing unit Mario Hlawitschka, Robert McGough, Katherine Ferrara, Dustin Kruse Abstract Book of the 2010 IEEE International Ultrasonics Symposium (IUS), San Diego, CA , IEEE, UFFC pp. 619, P5-M4-9 October 11-14 2010 [conference]
Abstract: In our preliminary work, we have demonstrated that ultrasonic drug release using mild hyperthermia is feasible; temperature sensitive drug delivery particles are injected and allowed to accumulate within a region of interest, typically over 6-24 hours. Ultrasound is then scanned through the volume of interest to locally increase the temperature by 2-4 degree celsius for a short period, releasing a drug and increasing its efficacy. In order to translate these methods, ultrasound AND drug dose must each be predicted and validated. We have made great strides on drug dose—we now tackle ultrasound dose for this special problem of mild hyperthermia. Predicting the 3-D heating profile in tissue as a function of time requires knowledge of the acoustic beam intensity as a function of time as it is steered in 3-D space. Ultrasound beams generated from an aperture large enough to deliver the acoustic power necessary for tissue heating must be focused to some degree in order to work at reasonable depths from the aperture face and at depth-of-fields that are not much larger that the desired heating region. Focusing necessitates that the beam be scanned in order to treat larger volumes, such as the volume encompassing a tumor. The beam scanning is accomplished dynamically, in real time, and knowledge of the beam is necessary in order to make predictions on where energy is being deposited and how much is being deposited. This information is important for predicting thermal dose according to Arrhenius-based methods such as Cumulative Equivalent Minutes at 43°C CEM4). In summary, we present our initial results using GPUs to accelerate the prediction of large-scale acoustic fields relevant to ultrasound hyperthermia. The FNM was chosen over other methods due to its rapid convergence and accuracy in the near- field up to the surface of the radiator. Algorithms for regularly-sampled 1-D and 2-D RSM Times (in milliseconds) FNM Times (in milliseconds) piston-arrays were presented and benchmarked to demonstrate the power of GPU- MinAccuracy 1.0% 0.1% 0.01% 1.0% 0.1% 0.01% Abscissas based field prediction for scenarios commonly found in ultrasound therapy. Our goal of generating the complex acoustic field for a volume containing 10 million points within 1 second is easily achieved using the algorithms and hardware presented. Our future goal is to incorporate this new ability into our ultrasound hyperthermia system for purposes of treatment planning and thermal dose prediction and control.
	Function approximations to accelerate 3-D beam predictions for thermal dose calculations. Dustin Kruse, Chun-Yen Lai, Mario Hlawitschka, Katherine Ferrara Proceedings of the 2009 IEEE International Ultrasonics Symposium pp. 1777-1779 September 20-23 2009 [ISBN: 978-1-4244-4389-5] [conference]
Abstract: We demonstrate that ultrasound beam predictions are accelerated by 22x using a fast approximation to evaluate complex exponentials with insignificant errors compared to full precision calculations. Since TAP is the more relevant quantity for thermal diffusion-limited heating, the small error of less than 0.1% indicates a better measure of the fast approximation compared to maximum intensity error of less than 1%. It appears in these preliminary results that errors in the beam prediction can be reduced by selecting a value for L closer to that which minimizes error for sine/cosine pairs based on the Pythagorean trigonometric identity. The same methodology may be applied to other beam prediction algorithms to speed their execution at a relatively minor degradation in accuracy.

Web Site Revisions

2011-02-04: Fixed missing semicolon in example code and corrected angle of view
2010-10-08: initial release