Zu jeder monotonen Grammatik G = ( M, A, R, S ) existiert ein
linear-beschränkter Automat B mit L (G) = L (B).
O.B.d.A. kann G als Kuroda-Normalform vorausgesetzt werden, wobei für die
Regeln (u, v) aus R gilt: 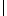 u
u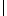 =
= 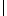 v
v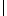
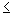 2 und u
2 und u 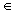 M
M 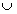 M2 und S nicht in v oder u = S und v
= Sy . Für jedes p
M2 und S nicht in v oder u = S und v
= Sy . Für jedes p 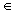 L
(G) gibt es dann eine Ableitung
L
(G) gibt es dann eine Ableitung
S 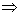 Sq
Sq 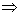 p mit
p mit 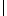 q
q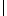 =
= 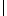 p
p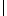 -1 , d.h., es wird zunächst ein mit S
beginnendes Wort der Länge von p aufgebaut. (Es ist nur ein Metazeichen m mit
q = m
-1 , d.h., es wird zunächst ein mit S
beginnendes Wort der Länge von p aufgebaut. (Es ist nur ein Metazeichen m mit
q = m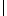 p
p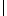 -1
erforderlich.)
-1
erforderlich.)
Man kann nun einen linear-beschränkten Automaten
B = ( A, Y, Z, h,
z0, F, [, ] ) angeben, wo h die längentreuen Regeln rückwärts
ausführt und das eingegebene Wort dann akzeptiert wird, wenn zwischen den
Randmarken ein Wort entsteht, daß mit den Regeln (S, v) 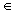 R aus S ableitbar ist.
R aus S ableitbar ist.
(Man kann auch einen Automaten mit einem zweispurigen Band konstruieren,
der auf der zweiten Spur nichtdeterministisch ein Wort aus L(G) erzeugt und
dieses dann mit dem auf der ersten Spur stehenden Eingabewort vergleicht. Der
Automat akzeptiert, wenn beide Spuren dasselbe Wort enthalten.)

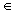 Y \ ( X
Y \ ( X 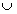 Z ) (linke bzw. rechte Randmarke) und
Z ) (linke bzw. rechte Randmarke) und
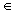 h (y, z) folgt y´ = [ bzw. ] genau dann,
wenn y = [ bzw. ]
h (y, z) folgt y´ = [ bzw. ] genau dann,
wenn y = [ bzw. ]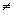 l bzw. r . (Die Randmarken dürfen
weder
l bzw. r . (Die Randmarken dürfen
weder
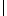 p
p 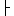 * [uzfv]
mit zf
* [uzfv]
mit zf 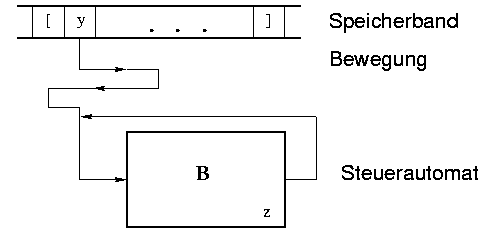
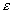 } = L gibt.
} = L gibt. 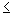 2 und u
2 und u 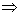 Sq
Sq 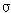 ,
, 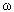 für x
für x